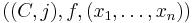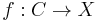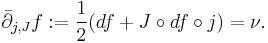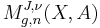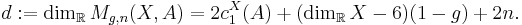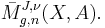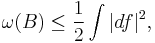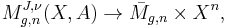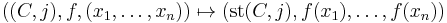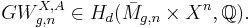Stable map
In mathematics, specifically in symplectic topology and algebraic geometry, one can construct the moduli space of stable maps, satisfying specified conditions, from Riemann surfaces into a given symplectic manifold. This moduli space is the essence of the Gromov–Witten invariants, which find application in enumerative geometry and type IIA string theory. Because the construction is lengthy and difficult, it is carried out here rather than in the Gromov–Witten invariants article itself.
Contents |
The moduli space of smooth pseudoholomorphic curves
Fix a closed symplectic manifold  with symplectic form
with symplectic form  . Let
. Let  and
and  be natural numbers (including zero) and
be natural numbers (including zero) and  a two-dimensional homology class in
a two-dimensional homology class in  . Then one may consider the set of pseudoholomorphic curves
. Then one may consider the set of pseudoholomorphic curves
where 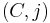 is a smooth, closed Riemann surface of genus
is a smooth, closed Riemann surface of genus  with
with  marked points
marked points  , and
, and
is a function satisfying, for some choice of  -tame almost complex structure
-tame almost complex structure 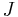 and inhomogeneous term
and inhomogeneous term  , the perturbed Cauchy–Riemann equation
, the perturbed Cauchy–Riemann equation
Typically one admits only those  and
and  that make the punctured Euler characteristic
that make the punctured Euler characteristic 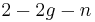 of
of  negative; then the domain is stable, meaning that there are only finitely many holomorphic automorphisms of
negative; then the domain is stable, meaning that there are only finitely many holomorphic automorphisms of  that preserve the marked points.
that preserve the marked points.
The operator  is elliptic and thus Fredholm. After significant analytical argument (completing in a suitable Sobolev norm, applying the implicit function theorem and Sard's theorem for Banach manifolds, and using elliptic regularity to recover smoothness) one can show that, for a generic choice of
is elliptic and thus Fredholm. After significant analytical argument (completing in a suitable Sobolev norm, applying the implicit function theorem and Sard's theorem for Banach manifolds, and using elliptic regularity to recover smoothness) one can show that, for a generic choice of  -tame
-tame 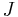 and perturbation
and perturbation  , the set of
, the set of 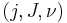 -holomorphic curves of genus
-holomorphic curves of genus  with
with  marked points that represent the class
marked points that represent the class  forms a smooth, oriented orbifold
forms a smooth, oriented orbifold
of dimension given by the Atiyah-Singer index theorem,
The stable map compactification
This moduli space of maps is not compact, because a sequence of curves can degenerate to a singular curve, which is not in the moduli space as we've defined it. This happens, for example, when the energy of  (meaning the L2-norm of the derivative) concentrates at some point on the domain. One can capture the energy by rescaling the map around the concentration point. The effect is to attach a sphere, called a bubble, to the original domain at the concentration point and to extend the map across the sphere. The rescaled map may still have energy concentrating at one or more points, so one must rescale iteratively, eventually attaching an entire bubble tree onto the original domain, with the map well-behaved on each smooth component of the new domain.
(meaning the L2-norm of the derivative) concentrates at some point on the domain. One can capture the energy by rescaling the map around the concentration point. The effect is to attach a sphere, called a bubble, to the original domain at the concentration point and to extend the map across the sphere. The rescaled map may still have energy concentrating at one or more points, so one must rescale iteratively, eventually attaching an entire bubble tree onto the original domain, with the map well-behaved on each smooth component of the new domain.
In order to make this precise, define a stable map to be a pseudoholomorphic map from a Riemann surface with at worst nodal singularities, such that there are only finitely many automorphisms of the map. Concretely, this means the following. A smooth component of a nodal Riemann surface is said to be stable if there are at most finitely many automorphisms preserving its marked and nodal points. Then a stable map is a pseudoholomorphic map with at least one stable domain component, such that for each of the other domain components
- the map is nonconstant on that component, or
- that component is stable.
It is significant that the domain of a stable map need not be a stable curve. However, one can contract its unstable components (iteratively) to produce a stable curve, called the stabilization 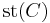 of the domain
of the domain  .
.
The set of all stable maps from Riemann surfaces of genus  with
with  marked points forms a moduli space
marked points forms a moduli space
The topology is defined by declaring that a sequence of stable maps converges if and only if
- their (stabilized) domains converge in the Deligne–Mumford moduli space of curves
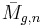 ,
, - they converge uniformly in all derivatives on compact subsets away from the nodes, and
- the energy concentrating at any point equals the energy in the bubble tree attached at that point in the limit map.
The moduli space of stable maps is compact; that is, any sequence of stable maps converges to a stable map. To show this, one iteratively rescales the sequence of maps. At each iteration there is a new limit domain, possibly singular, with less energy concentration than in the previous iteration. At this step the symplectic form  enters in a crucial way. The energy of any smooth map representing the homology class
enters in a crucial way. The energy of any smooth map representing the homology class  is bounded below by the symplectic area
is bounded below by the symplectic area 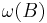 ,
,
with equality if and only if the map is pseudoholomorphic. This bounds the energy captured in each iteration of the rescaling and thus implies that only finitely many rescalings are needed to capture all of the energy. In the end, the limit map on the new limit domain is stable.
The compactified space is again a smooth, oriented orbifold. Maps with nontrivial automorphisms correspond to points with isotropy in the orbifold.
The Gromov–Witten pseudocycle
To construct Gromov–Witten invariants, one pushes the moduli space of stable maps forward under the evaluation map
to obtain, under suitable conditions, a rational homology class
Rational coefficients are necessary because the moduli space is an orbifold. The homology class defined by the evaluation map is independent of the choice of generic  -tame
-tame 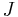 and perturbation
and perturbation  . It is called the Gromov–Witten (GW) invariant of
. It is called the Gromov–Witten (GW) invariant of  for the given data
for the given data  ,
,  , and
, and  . A cobordism argument can be used to show that this homology class is independent of the choice of
. A cobordism argument can be used to show that this homology class is independent of the choice of  , up to isotopy. Thus Gromov–Witten invariants are invariants of symplectic isotopy classes of symplectic manifolds.
, up to isotopy. Thus Gromov–Witten invariants are invariants of symplectic isotopy classes of symplectic manifolds.
The "suitable conditions" are rather subtle, primarily because multiply covered maps (maps that factor through a branched covering of the domain) can form moduli spaces of larger dimension than expected.
The simplest way to handle this is to assume that the target manifold  is semipositive or Fano in a certain sense. This assumption is chosen exactly so that the moduli space of multiply covered maps has codimension at least two in the space of non-multiply-covered maps. Then the image of the evaluation map forms a pseudocycle, which induces a well-defined homology class of the expected dimension.
is semipositive or Fano in a certain sense. This assumption is chosen exactly so that the moduli space of multiply covered maps has codimension at least two in the space of non-multiply-covered maps. Then the image of the evaluation map forms a pseudocycle, which induces a well-defined homology class of the expected dimension.
Defining Gromov–Witten invariants without assuming some kind of semipositivity requires a difficult, technical construction known as the virtual moduli cycle.
References
- Dusa McDuff and Dietmar Salamon, J-Holomorphic Curves and Symplectic Topology, American Mathematical Society colloquium publications, 2004. ISBN 0-8218-3485-1.